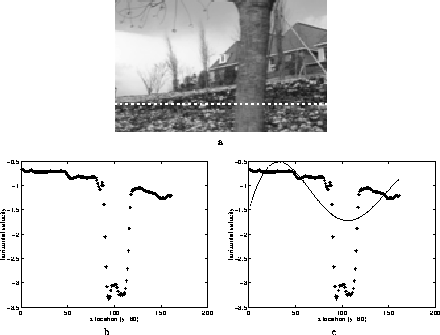



Figure 15: The integration versus segmentation dilemma in natural
images. a. A single frame from the MPEG flower garden
sequence. The sequence was shot by a camera placed on a driving car,
and the image motion is related to distance from the camera. Thus the
tree, which is closest to the camera moves
fastest. b. The output of
state-of-the art local motion analyzer on this
scene [Bergen et al., 1992]. We show the horizontal estimated
velocity at a cross section of the image. Note that even
though all locations are textured and hence contain multiple
orientations, the estimated local flow is still quite noisy.
c. The output of a global smoothness algorithm on this
sequence. The tree is predicted to move much slower than it
really does because its motion is combined with that of the flowers.
The algorithm is integrating constraints that
should be segmented.
Figure 16: The output of motion segmentation algorithms
on the flower garden sequence.
b. A cross section through the horizontal flow field predicted
by the Wang and Adelson (1994) algorithm. Although the algorithm segments the
tree from the flowers, the motion of each layer is flat as if it were
made of cardboard.
c. A cross section through the horizontal flow field predicted
by the smoothness in layers algorithm. Note that the algorithm
more accurately captures the curved shape of the tree and the flower beds.
In section 1 we discussed the inherent ambiguity of local motion measurements. For the synthetic ideal images we discussed the ambiguity only occurs at locations containing a single orientation. Locations such as corners, where multiple orientations exist locally, are unambiguous. However, in the presence of noise, all local measurements are ambiguous --- even if the location contains multiple orientations the extraction of the correct constraints is limited by the noise in the image. Thus in a noisy world, the distinction between ``corners'' and ``lines'' is a slightly artificial dichotomy --- all locations have some ambiguity. Rather than ``ambiguous'' versus ``unambiguous'' locations, in a noisy world the degree of ambiguity of local measurements may take on a continuum of values.
Figure 15 shows an example of the ambiguity of local measurements in real world scenes. The sequence was shot by a camera placed on a driving car, and the image motion is related to distance from the camera. Thus the tree, which is closest to the camera moves fastest. Figure 15a shows the output of state-of-the art local motion analyzer on this scene [Bergen et al., 1992]. We show the horizontal estimated velocity at a cross section of the image. The pixels corresponding to the tree move fastest and the background pixels corresponding to the flower bed move with spatially varying slower speed. Note that even though all locations are textured and hence contain multiple orientations, the estimated local flow is still quite noisy. At the border of the tree and the flower garden the local analysis gives an intermediate velocity that is quite different from the true image motion, and along the flower bed the local estimate varies noisily from location to location in a way that does not reflect the true depth of the scene. Figure 15c shows the output of a global smoothness algorithm on this sequence. Again we show the only the horizontal estimated flow along a cross section. Now the estimate is highly smooth but quite wrong. Since the algorithm assumes a smoothly varying velocity field, the tree is predicted to move much slower than it really does. Its motion is influenced by the motion of the slowly moving flowers. This is precisely the integration versus segmentation dilemma --- deriving reliable estimates requires integrating information from multiple locations while segmenting information derived from different motions.
The problems with global smoothness approaches are well known and have prompted a recent trend in computer vision towards approaches that fit multiple, global motion models to the image data. [Darrell and Pentland, 1991,Jepson and Black, 1993,Irani and Peleg, 1992,Hsu et al., 1994,Ayer and Sawhney, 1995,Wang and Adelson, 1994]. While differing in implementation, these algorithms share the goal of deriving from the image data a representation consisting of (1) a small number of global motion models and (2) a segmentation map that indicates which pixels are assigned to which model.
In order to segment images based on common motion, most existing algorithms assume that the motion of each model is described by a low dimensional parameterization. The two most popular choices are a six parameter affine model [Wang and Adelson, 1994,Weiss and Adelson, 1996] or an eight parameter projective model [Ayer and Sawhney, 1995,Irani and Peleg, 1992]. Both of these parameterizations correspond to the rigid motion of a plane: the affine model assumes orthographic projection while the projective model assumes a perspective projection.
Despite the success of existing algorithms in segmenting image sequences, the assumption that motion segments correspond to rigid planar patches is obviously restrictive. Non-planar surfaces, or objects undergoing non-rigid motion cannot be grouped. Even when the segmentation is correct, the restriction to planar motions means that the estimated motion for each segment may be wrong. Figure 16b shows the estimated motion from a segmentation algorithm that assumes planar motions [Wang and Adelson, 1994,Ayer and Sawhney, 1995,Weiss and Adelson, 1996]. Figure 16b shows a cross section from the estimated flow --- at each location we plot the horizontal velocity of the segment to which that location belongs. Note that unlike the global smoothness approach, the tree does not ``pull along'' portions of the flower bed. The constraints from the tree and the bed are segmented rather than integrated. However, the motion of the tree and the flower bed are both approximated by planar motions --- as if they were painted on flat sheets of cardboard.
In the third part of the thesis we show that the ``smoothness in layers'' assumption can be used to segment such scenes. We present an algorithm that segments such scenes and estimates a smooth motion field for each layer or segment rather than a low-dimensional parametric flow field. We combine the ideas of smoothness and segmentation in a mixture model framework, and this leads to an efficient Expectation-Maximization (EM) algorithm. An additional advantage of the mixture estimation framework is that additional cues for segmentation can be incorporated in a natural fashion. Figure 16c shows the output of our algorithm on the flower garden sequence. The segmentation is similar to the one obtained using planar motions but the estimated motion is rather different. Unlike the planar models, the velocity fields have enough degrees of freedom in order to capture the curved nature of the tree and the flower bed. Unlike the global smoothness algorithm, the algorithm avoids mixing together constraints derived from different objects. These results suggest that the same assumptions used in modeling the psychophysical result may also be useful in improving the performance of computer vision systems.


