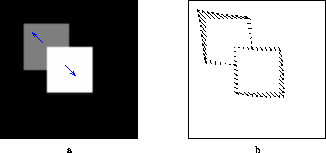



Figure 8: a. Two squares translate in the image in different
directions.
b. The output of a
standard smoothness algorithm on this sequence. The algorithm tries to
simultaneously fit the motion of both surfaces and recovers a single
elastic deformation that is not at all like the human percept.
In the second part of the thesis, we address the larger question --- simultaneous integration and segmentation of motion constraints. The first part showed that the assumption of slow and smooth velocity fields can account for the human percept in a wide range of scenes containing a single motion. However, if the scene contains multiple objects, the ``slow and smooth'' assumption predicts percepts that are nothing like the human percept. Figure 8 shows the predicted velocity for the two squares scene -- while humans perceive two rigid bodies, the ``slow and smooth'' assumption predicts a single, elastically deforming body. In the second part of the thesis we present an extension of the ``slow and smooth'' assumption to scenes containing multiple motions.
The failure of global smoothness algorithms in scenes containing multiple motions such as figure 8 is well known and several ways of fixing the smoothness assumption have been proposed. Hildreth (1983) proposed a model whereby smoothness is only assumed along contours. Her algorithm found the velocity field of least variation along the zero crossings of the image. To illustrate her assumption consider the two squares scene discussed in figure 8. Hildreth's algorithm would first extract contours from this scene and then combine measurements along the contour. Thus assuming that the first step correctly extracted two contours, one for the boundary of each square, her algorithm would only assume smoothness in the motion of each square. It would not assume any relationship between the motions of the two squares. Thus for this stimulus it would predict two rigid motions, consistent with human perception.
Although Hildreth's assumption of smoothness along contours does solve some of the problems associated with smoothness models, there is reason to believe it is not exactly the assumption used by the human visual system. As pointed out by Grzywacz and Yuille (1991) the Hildreth assumption would predict no influence between features that are off the contour and the perceived motion of the contour. This is inconsistent with experimental results that show a strong influence of features in such displays (e.g.[Nakayama and Silverman, 1988a,Shiffrar et al., 1995,Weiss and Adelson, 1995,Rubin and Hochstein, 1993]). Figure 9 shows an example dating back to Wallach (1935). A line whose endpoints are invisible appears to move in the normal direction, but when a small number of dots translating horizontally are added to the display they tend to ``capture'' the line, and the line appears to move horizontally. The fact that the dot influences the line when it is not part of the line's contour is inconsistent with Hildreth's model or any other model that assumes smoothness only along contours.
Figure 9: a. A horizontally translating diagonal line whose
endpoints are invisible is consistent with an infinite family of
motions. Typically, under these conditions, the normal velocity is
chosen and the line appears to translate diagonally. (Wallach 35)
b. When two horizontally translating dots are added to the
display the line appears to move in the direction of the dots (Wallach
35, Rubin and Hochstein 93). This is inconsistent with a model that
only combines information along contours (e.g. Hildreth 83).
c. The effect persists when the display is placed on a static
texture background. This is inconsistent with
an algorithm that assumes ``smoothness with discontinuities''
(e.g. Terzopoulos 86). The discontinuities formed between the dots and
the background would inhibit any interactions between the dots and the
line.
Rather than restricting the smoothness assumption to contours, other approaches assume a smooth two dimensional velocity field with possible discontinuities. In these models, e.g. [Terzopoulos, 1986,Hutchinson et al., 1988,Horn, 1986], nearby points are assumed to have similar velocities, but if the velocities are too dissimilar the assumption is abandoned and a discontinuity is assumed there instead. An advantage of these models over the standard smoothness models is that when the location of the discontinuity is estimated correctly, there is no smoothing across boundaries. This avoids many of the oversmoothing problems associated with global smoothness algorithms.
Despite these successes, there exist scenes in which the discontinuities approach predicts a motion that is very different from the human percept. Essentially, it predicts no interaction between two locations if there is a motion discontinuity between them. Figure 9c shows a simple example in which the line and the dot translate horizontally over a static background.The dissimilarity between the motions of the dots and the background texture would give rise to a discontinuity as would the dissimilarity between the line and the texture. Yet human perceiving this scene report no difference between the percept with and without the static texture. The dots and the line appear to be in front of the texture and are perceived as a single surface. Thus while piecewise smoothness may be a reasonable assumption to make in many contexts, it does not appear to be sufficient for modeling human motion perception.
As these simple demonstrations show, the visual system does not appear to assume global smoothness over the image, nor does it assume smoothness only along contours, nor does it assume smoothness with discontinuities. In the second part of the thesis, we propose a formulation that we call ``smoothness in layers''. We assume the scene includes a small number of surfaces or layers [Wang and Adelson, 1994] and that motion varies smoothly within a given layer. To illustrate this assumption consider figure 10. Global smoothness would assume that motion varies smoothly over the entire image, while smoothness in layers assumes that one velocity field will vary smoothly over the front surface and a second velocity field will vary smoothly over the back surface. There is no assumption of smoothness between two layers only within layers. This distinction is illustrated in a 1D example in figure 11
Unfortunately, the input to the visual system is not a description in terms of surfaces or layers. Thus if we wish to account for human motion perception by assuming smoothness in layers, we need to also account for the formation of a layered description from spatiotemporal data. In the second part of the thesis we present a computational model that receives as input a gray level image sequence and calculates (1) the number of layers (2) the assignment of pixels to layers and (3) the velocity field of each layer.
Figure 10: Layered decomposition of image sequences (adapted
from [Wang and Adelson, 1994]). In a layered description, an
image sequence is decomposed into a small number of occluding layers
or surfaces, and each layer has a corresponding motion field. In this
paper we propose that human motion perception assumes the motion field
of each layer is smooth, but does not assume smoothness between motion
fields of different layers.
Figure 11: An illustration of the smoothness in layers assumption in
1D (adapted from [Wang and Adelson, 1994]). a.
Hypothetical velocity estimates as a function of position. Such data
would typically arise from two surfaces in depth. b.
Global smoothness assumption applied to this data. The
measurements from the two surfaces are mixed together rather than
segmented. c. Piecewise smoothness. Information is
not propagated across discontinuities. The resulting estimate is
rather noisy. d. Smoothness in Layers. Two smooth velocity
functions are found, one for each surface.
The model uses the statistical framework of mixture estimation to find the most probable interpretation of a scene. It is based on three assumptions: (1) a likelihood term identical to the one used in the first part that assumes image measurements may be noisy (2) a prior term that favors slow and smooth velocity fields within a layer and (3) a preference for a small number of layers. In order to validate these assumptions, we compare the most probable interpretation under these assumption to human percepts in previously published stimuli.
As an example of the type of data we would like to account for, consider figure 12. When the plaid on the left is shown to human subjects, they tend to see two motions --- the plaid does not cohere but each grating is seen as moving in its normal direction. However when the plaid on the right is presented, subjects tend to see a single, coherent pattern translating in the horizontal direction. The tendency of plaids to cohere or appear transparent has been widely studied and has shown to be influenced by speed, period, orientation and contrast [Adelson and Movshon, 1982,Kim and Wilson, 1993,Farid and Simoncelli, 1994]. As we show in the second part of the thesis, these tendencies are predicted from the three assumptions outlined above --- there is no need for stimulus specific heuristics.
Figure 12: Adelson and Movshon (1982) found that the tendency of
plaids to cohere depended on the difference between the principal
direction of the two gratings. Thus the plaid in a tends to
cohere less than the plaid in b. In the second part of the
thesis we show that this tendency is predicted by the assumption of
``smoothness in layers''.
Figure 13: The split herringbone illusion [Adelson and Movshon, 1983]. Two sets of diagonal lines translate
vertically in opposite directions. At high
contrast [Adelson and Movshon, 1983] the percept consists of two groups,
one moving up and the other moving down. However, if the stimulus is
blurred, viewed peripherally or at low contrast, one
perceives a single coherent motion to the right. In the second part of
the thesis, we show that this ``illusion'' is the most probable
percept given the ``smoothness in layers'' assumption.
Although plaids present the most widely studied stimuli in which humans were asked to judge whether one or two motions were present, the ``smoothness in layers'' assumption is by no means restricted to plaid stimuli. Figure 13 shows the split herringbone illusion [Adelson and Movshon, 1983]. Two sets of diagonal lines translate vertically in opposite directions. At high contrast [Adelson and Movshon, 1983] the percept consists of two groups, one moving up and the other moving down. However, if the stimulus is blurred, viewed peripherally or at low contrast, one perceives a single coherent motion to the right. As we show in the second part, this ``illusory'' motion at low contrast is actually the most probable interpretation given the assumption of smoothness in layers.
Figure 14: When a ``fat'' ellipse rotates rigidly in the image plane
it is perceived as deforming nonrigidly [Wallach et al., 1956]. When four
rotating dots are added to the display, the ellipse is perceived as
rigid [Weiss and Adelson, 1995]. The effect of the satellites persists
when a large number of vertically translating dots is added to the
display [Weiss and Adelson, 1995]. In the second part of the thesis we
show that this is also predicted by the ``smoothness in layers'' assumption.
Since we estimate a smooth velocity field for every layer, the smoothness in layers assumption can be applied to scenes in which the objects are undergoing nontranslational motions. Figure 14 shows an example with the ellipse stimulus discussed earlier. When a ``fat'' ellipse rotates rigidly in the image plane it is perceived as deforming nonrigidly [Wallach et al., 1956]. When four rotating dots are added to the display, the ellipse and the dots are perceived as moving together and the ellipse is perceived as rigid [Weiss and Adelson, 1995]. The effect of the four satellites persists when a large number of vertically translating dots is added to the display [Weiss and Adelson, 1995]. In this case, humans perceive two groups --- the ellipse and the four dots are perceived as moving together but the vertically translating dots are perceived as being in a separate layer. As we show in the second part of the thesis, this tendency is also predicted by the smoothness in layers assumption.
Despite the success of the smoothness in layers assumption in accounting for a wide range of stimuli, there exist stimuli for which these three assumptions are not sufficient. The second part of the thesis also discusses these shortcomings. There are many non-motion cues that influence the tendency of humans to segment or integrate motion measurements. For example in the case of plaids, cues such as stereo depth, the luminance of the intersections and the relative spatial frequencies cause the plaid to appear more transparent [Adelson and Movshon, 1982,Stoner et al., 1990,Bressan et al., 1993]. These cues increase the tendency to see the plaid as two transparent gratings even in a single static frame, and the three assumptions discussed above know nothing about this static analysis. We discuss how to augment these assumptions so they can incorporate additional cues and show preliminary results with the more sophisticated set of assumptions.


