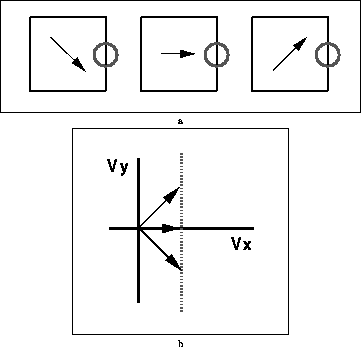



Figure 1: a. The ``aperture problem'' refers to the
impossibility of determining the two dimensional motion of a signal containing a
single orientation. Given a vertical edge, only the horizontal
component of motion
can be determined. b. The family of motions consistent with the motion of the
edge can be depicted as a line in ``velocity space'', where any
velocity is represented as a vector from the origin whose length is
proportional to speed and whose angle corresponds to direction of
motion.
Figure 2: a. A single translating figure generates different constraints
at different locations. b. When the constraints are plotted together
they intersect at a single point yielding
the physically correct velocity of the square. This is an example of how
integrating multiple constraints can resolve the local ambiguity of
motion measurements.
Figure 3: a. When the scene contains multiple objects, a simple
velocity space construction is not sufficient to determine the
motions. b. When the constraints from multiple locations are
plotted together they intersect at four points. Two of these points
correspond to
the motion of a square, while the other two are spurious --- they
result from integrating together constraints that belong to different
objects. This simple scene illustrates
the need to simultaneously integrate and segment motion measurements.
In this thesis we seek to understand how the human visual system solves what we call ``the integration versus segmentation dilemma''. This dilemma arises from the conflicting demands of motion analysis in scenes containing multiple motions [Braddick, 1993]. Due to the inherent ambiguity of local motion measurements, local computations do not gather enough information to obtain a correct estimate. Thus the system needs to integrate many local measurements. On the other hand, the fact that there are multiple motions means that global computations are likely to mix together measurements derived from different motions. Thus the system needs to segment the local measurements.
To illustrate these conflicting demands consider the simple scenes depicted in figures 1 through 3. Figure 1 shows the inherent ambiguity of local motion measurements. The well known ``aperture problem'' [Wallach, 1935,Horn and Schunck, 1981,Adelson and Movshon, 1982,Marr and Ullman, 1981,Fennema and Thompson, 1979] refers to the impossibility of determining the two dimensional motion when a signal only contains a single orientation. For example, a local analyzer that sees only the vertical edge of a square can only determine the horizontal component of the motion. Whether the square translates horizontally to the right, diagonally up and to the right, or diagonally down and to the right, the motion of the vertical edge will be the same. The family of motions consistent with the motion of the edge can be depicted as a line in ``velocity space'', where any velocity is represented as a vector from the origin whose length is proportional to speed and whose angle corresponds to direction of motion. Graphically, the aperture problem is equivalent to saying that the family of motions consistent with the information at an edge maps to a straight line in velocity space, rather than a single point.
This ambiguity may be reduced by combining information over space. Figure 2a shows velocity space representations of constraints from different image locations along the square. At an edge, the constraint is a line in velocity space with the same orientation as the edge, while at a corner, the constraint is a point in velocity space --- there is a single velocity consistent with the local data. Figure 2b shows all of these constraints plotted in single representation --- they all intersect at a single point, and that intersection gives the physically correct velocity of the square.
If the visual system only needed to analyze motion in scenes containing a single object, it would only need to solve the integration problem, and not the segmentation problem. When the scene contains multiple objects, however, the situation is more complex. Figure 3 shows an example (after [Burt and Sperling, 1981]). Here there are two squares translating in different directions. As in the one-square case, measurements along the edge are ambiguous while measurements obtained at junctions are not. However, unlike the one-square case, the unambiguous measurements do not necessarily correspond to the correct motion of either square. Furthermore, when the constraints are plotted together they do not intersect at a single point. Rather four intersections are found. Two of these points correspond to the correct motions of the two squares. The other two points, however, do not correspond to any ``true'' motion in the scene. They are a result of mixing together constraints derived from different objects, of integrating together measurements that should be segmented.
As we show in this thesis, the simple two squares scene presents a problem for many computer vision motion analysis systems. Local motion analyzers cannot overcome the local ambiguity along the edges of the squares, while global approaches tend to mix together information belonging to different squares and predict an incorrect motion. Yet humans perceiving this scene have no trouble in indicating the motion at different points in the scene; the human visual system seems to have found a way to resolve the integration versus segmentation dilemma. The focus of this thesis is to understand this performance.


