


Rather than immediately taking on the full ``integration versus segmentation'' dilemma, the first part of the thesis deals only with the problem of integration. We address situations in which subjects are told that there is only a single moving surface in the scene and are asked to judge that motion. Thus there is no segmentation problem. The system still has to combine multiple local measurements to arrive at the motion of the surface. The first part asks how the human visual system performs this combination.
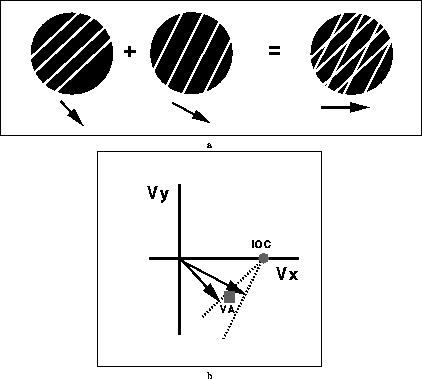
As mentioned in the introduction, given a stimulus with only a single orientation there is not enough information to find the two dimensional velocity vector. However, assuming the stimulus is translating in the image plane, two orientations should be sufficient to determine its velocity. Perhaps the simplest stimulus containing two orientations is the ``plaid'' stimulus in which two oriented gratings translate rigidly in the image plane (figure 5a). Due to the aperture problem, only the component of velocity normal to the orientation of the grating can be estimated, and hence each grating motion is consistent with an infinite number of possible velocities, a constraint line in velocity space (figure 5b). When each grating is viewed in isolation, subjects typically perceive the normal velocity (shown by arrows in figure 5b). Yet when the two gratings are presented simultaneously subjects often perceive them moving coherently and ascribe a single motion to the plaid pattern [Adelson and Movshon, 1982,Wallach, 1935].
Figure 5: a. Two translating gratings form a ``plaid''
stimulus. Each grating by itself contains only a single
orientation and its motion can not be estimated uniquely. However when
both gratings are added, subjects often assign a single motion to the
pattern [Adelson and Movshon, 1982,Wallach, 1935]. For this reason, plaid stimuli are often used to study the
method by which humans combine multiple motion measurements.
b. Two velocity space constructions that could be used
to estimate this ``pattern motion'' -- Intersection of Constraints
(IOC) and Vector Average (VA). Neither of these mechanisms are
sufficient to to explain the experimental data on
perceived direction of plaids. In the first part of the thesis we
present a single computational mechanism that can explain the range of percepts.
Adelson and Movshon (1982) distinguished between three methods to estimate this ``pattern motion'' -- Intersection of Constraints (IOC), Vector Average (VA) and blob tracking. Intersection of Constraints (IOC) finds the single translation vector that is consistent with the information at both gratings. Graphically, this can be thought of as finding the point in velocity space that lies at the intersection of both constraint lines (circle in figure 5b). Vector Average (VA) combines the two normal velocities by taking their average. Graphically this corresponds to finding the point in velocity space that lies halfway in between the two normal velocities (square in figure 5b). Blob tracking makes use of the motion of the intersections [Ferrera and Wilson, 1990,Mingolla et al., 1992] which contain unambiguous information indicating the pattern velocity. For plaid patterns blob tracking and IOC give identical predictions --- they would both predict veridical perception.
The wealth of experimental results on the perception of motion in plaids reveals a surprisingly complex picture. Perceived pattern motion is sometimes veridical (consistent with IOC or feature tracking) and at other times significantly biased towards the VA direction. The degree of bias is influenced by factors including orientation of the gratings [Yo and Wilson, 1992,Bowns, 1996,Burke and Wenderoth, 1993], contrast [Stone et al., 1990], presentation time [Yo and Wilson, 1992] and foveal location [Yo and Wilson, 1992].
Figure 6: The insufficiency of either VA, IOC or feature tracking to
explain the human percept. a. A ``narrow'' rhombus whose
endpoints are occluded appears to move diagonally (consistent with
VA). b. A ``fat'' rhombus whose endpoints are occluded appears
to move horizontally (consistent with IOC or feature tracking).
c. A high contrast ``narrow'' rhombus with visible endpoints appears to move
horizontally (consistent with IOC or feature tracking). d. A
low contrast ``narrow'' rhombus with visible endpoints appears to move
diagonally (consistent with VA). In the first part of the thesis we
show how these results are predicted by a single, simple model based
on a few assumptions.
Figure 7: a. a ``fat'' ellipse rotating rigidly in
the image plane appears to deform nonrigidly.
b. a ``narrow'' ellipse rotating rigidly in the image plane
appears to rotate rigidly. In the first part of the thesis we show
that this phenomena is predicted by
that the same assumptions that predict biases in perceived velocity of
plaids and rhombuses.
The insufficiency of any of the three mechanisms to explain the human percept may also be illustrated using the horizontally translating rhombus stimulus in figure 6. Although slightly more complicated than the plaid stimulus, the rhombus also contains only two orientations and may be used to test the three mechanisms suggested by Adelson and Movshon. A ``narrow'' rhombus whose corners are occluded (figure 6a) appears to move diagonally and is therefore consistent with VA but inconsistent with IOC or feature tracking. A ``fat'' rhombus whose corners are occluded (figure 6b) appears to move horizontally and is therefore consistent with IOC or feature tracking but not with VA. When the corners are visible (figure 6c) and the contrast is high the rhombus appears to move horizontally, but when the contrast is low it appears to move diagonally.
Thus even for very simple stimuli, the question of which combination rule is used by human subjects is not easily answered. Conventional explanations involve multiple mechanisms, each invoked in order to explain a portion of the psychophysical results. The situation becomes even more complex when we consider non-translational motions. As an example, consider the perception of circles and derived figures in rotation (figure 7). When a ``fat'' ellipse , with aspect ratio close to unity, rotates in the image plane, it is perceived as deforming nonrigidly [Musatti, 1924,Wallach et al., 1956,Musatti, 1975]. However, when a ``narrow'' ellipse, with aspect ratio far from unity, rotates in the image plane, the motion is perceived veridically [Wallach et al., 1956].
Obviously, none of the three mechanisms suggested for perception of plaids can be directly applied to explain this percept. These models estimate a single velocity vector rather than a spatially varying velocity field. An elegant explanation of the ellipse phenomena was offered by Hildreth (1983) using a very different style of model. She explained this and other motion ``illusions'' of smooth contours with a model that minimizes the variation of the perceived velocity field along the contour. She showed that for a rigid body with explicit features, her model will always give the physically ``correct'' motion field, but for smooth contours the estimate may be wrong. In the cases when the estimate was physically ``wrong'', it qualitatively agreed with human percepts of the same stimuli. Grzywacz and Yuille (1991) used a modified definition of smoothness to explain the misperception of smooth contours undergoing rigid translation [Nakayama and Silverman, 1988a,Nakayama and Silverman, 1988b]. Poggio et al. (85) have shown that the smoothness assumption is useful in many aspects of computational vision.
In the first part of the thesis, we show that a single, simple model based on a small number of assumptions can account for a wide range of percepts. The model is essentially based on only two assumptions: (1) a likelihood term that assumes that image measurements may be noisy and (2) a prior term that favors slow and smooth velocity fields. We calculate the velocity field that maximizes the posterior probability and compare this prediction to the percept of human observers. In reviewing a long list of previously published phenomena, we find that the Bayesian estimator almost always predicts the psychophysical results. The predictions agree qualitatively, and are often in remarkable agreement quantitatively.


