In this exercise we analyze a system with two servers, similar to those we talked about in class.
Consider a system with two servers, with a service rate of 1 (that is,
they serve one customer per unit time on average).
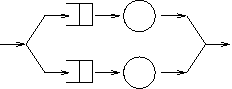Each server has its own queue.
Clients arrive at an average rate of 1.5 clients per unit time,
and select a server at random.
To simplify the analysis we will assume a maximum of 3 clients in the
system; if additional clients arrive when there are already 3 in the
system they simply give up immediately and do not enter the system at
all.
Interarrival and service time distributions are exponential.
Our goal is to analyze this system, and in particular to find the throughput and average response time. To do so, we need to delineate the possible system states, and find the long-term probability to be in each of them.
Note that the state space is two-dimensional, where state (n,m) represents n clients at the first server and m at the second server. The possible states are those for which n+m <= 3. The transitions between the states reflect new client arrivals or the departure of clients who have finished receiving service.
Note that this system has lots of symmetry, so actually there are not that many different probabilities and equations. In particular, in this specific case "local balance" applies. This means that if there is a transition from state A to state B, there is also an opposite transition from B to A, and moreover, that these two flows balance out. So if the probabilities to be in states A and B are PA and PB, and the transition rates are RAB and RBA, we have the equality PA RAB = PB RBA.
Recall also that the sum of the probabilities to be in all the states is 1.
The throughput is the rate at which clients receive service. For states with one busy server, this is equal to the service rate. For states with two busy servers, it is twice the service rate. The overall throughput is the weighted sum of this over all states, where the weights are the probabilities to be in the different states.
We can also calculate the expected number of clients in the system, by noting how many there are in each state, and what the probability for each state is.
The average response time is then given by Little's Law as the average number of clients in the system divided by the throughput.
Use Moodle to submit a report on your work, in pdf format, with the following data. Alternatively, you may also write the report by hand and submit it to me to avoid the need to type the equations and draw the graph of states and transitions on a computer. But if you do so it has to be very tidy.